Absolute Value Function
Summary —
Absolute Value Function f(x) = |x|
The graph of f(x) = |x| has a
shape.
• A negative in front of the absolute value, as in f(x) = -|x|, causes the vee to be inverted, like this
.
• A number added or subtracted inside the absolute value symbols,
as in f(x) = |x + h| or f(x) = |x - h|, shifts the
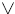horizontally by
h units.
For example:
• The graph of f(x) = |x + 4| is shifted 4 units to the left.
• The graph of f(x) = |x - 3| is shifted 3 units to the right.
• A number added or subtracted outside the absolute value
symbols, as in f(x) = |x| + k or f(x) = |x| - k, shifts the
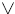vertically by k units.
For example:
• The graph of f(x) = |x| + 2 is shifted 2 units up.
• The graph of f(x) = |x| - 1 is shifted 1 unit down.
To determine the direction of a horizontal shift, it may be helpful to
rewrite the expression inside the absolute value symbols in the following
ways:
|
Form: f(x)
Example: f(x)
|
= |x + h|
= | x + 4|
= | x - (-4)| |
Form: f(x)
Example: f(x) |
= |x - h|
= |x - 3|
= |x - (+3)| |
| Here, h = -4. So, the graph
is shifted 4 units to the left. |
Here, h = +3. So, the graph
is shifted 3 units to the right. |
Example
Graph f(x) = |x + 2| + 3. Determine its domain and range.
Solution
We could calculate and plot points. However, from the above discussion
we know that this graph will be the same as the graph of f(x) = |x| but
shifted 2 units to the left (the 2 is added to the x) and 3 units
up (the 3 is added to the absolute value).
The domain is all real numbers.
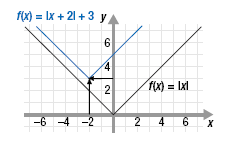
From the graph we can see that the y-coordinate of the vertex is 3 and the
vee opens upward. Therefore, range is y ≥ 3.
