Higher Degree Polynomial Functions

A Polynomial Function is a function of the form:

f(x) = a_n xⁿ + a_{n - 1} x^{n - 1}+ a_{n - 2} x^{n - 2} + ... + a₁ x + a₀

where the a's are real numbers and n is a non-negative integer.

Domains: (-∞, ∞)

Ranges: vary

Degree of a polynomial function is n.

The GRAPHS of polynomial functions are smooth, continuous curves, with no sharp turns.

Cubic Functions are third degree polynomial functions.

The turning points are called Local Extreme Points, or Local Extrema.

Sometimes we are interested in finding the highest or lowest point on the graph of a function over a certain interval. These points are called absolute maximum or absolute minimum points. 

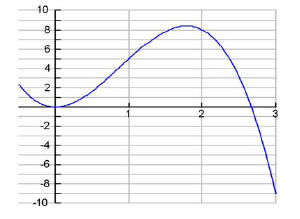
For example, if we graphed the cubic function f(x) = -3x³ + 8x² over the interval [ -0.5, 3], this is what we would get:

Quartic Functions are fourth degree polynomial functions. 

In general, we can tell certain things about polynomial functions just from looking at their equations. We can tell the maximum possible number of x-intercepts and turning points.

For an nth degree polynomial function:

The maximum number of x-intercepts is n.

The maximum number of turning points is n - 1.

We can also tell about the end behavior of polynomial functions. A cubic function will have ends that go in opposite directions, while a quartic function will have ends that either both go up or both go down. The leading coefficient determines the end behavior.

Function	Possible Graphs		Degree	Turning points	End Behavior		Degree Even or Odd
					possitive leading coefficient	negative leading coefficient
Linear	Positive slope	Negative slope	1	0			odd
Quadratic	Possitive leading coefficient	Negative leading coefficient	2	1			even
Cubic	Positive leading coefficient Negative leading coefficient		3	2 or 0			odd
Quartic	Positive leading coefficient Negative leading coefficient		4	3 or 1			even