Solving Systems of Equations by Graphing
Any collection of two or more equations is called a
system of equations. If the equations of a system involve two variables, then the set
of ordered pairs that satisfy all of the equations is the solution set of the system. In
this section we solve systems of linear equations in two variables.
Solving a System by Graphing
Because the graph of each linear equation is a line, points that satisfy both equations
lie on both lines. For some systems these points can be found by graphing.
Example 1
A system with only one solution
Solve the system by graphing:
y = x + 2
x + y = 4
Solution
First write the equations in slope-intercept form:
y = x + 2
y = -x + 4
Use the y-intercept and the slope to graph each line. The graph of the system is
shown in the figure below.
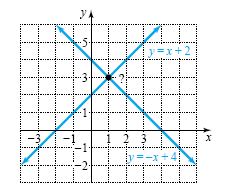
From the graph it appears that these lines intersect at
(1, 3). To be certain, we can check that (1, 3) satisfies both equations. Let x
= 1 and
y = 3 in y = x + 2 to get
3 = 1 + 2.
Let x = 1 and y = 3 in x + y = 4 to get
1 + 3 = 4.
Because (1, 3) satisfies both equations, the solution set to the system is {(1, 3)}.
The graphs of the equations in the next example are parallel lines, and there is
no point of intersection.
Example 2
A system with no solution
Solve the system by graphing:
2x - 3y = 6
3y - 2x = 3
Solution
First write each equation in slope-intercept form:
| 2x - 3y |
= 6 |
3y - 2x |
= 3 |
| -3y |
= -2x + 6 |
3y |
= 2x + 3 |
| y |
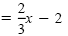 |
y |
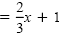 |
The graph of the system is shown in the next figure.
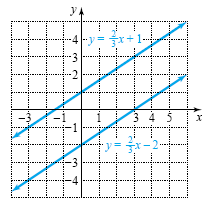
Because the two lines in this figure are parallel, there is no ordered pair that satisfies both equations. The solution set to the
system is the empty set, Ø.
The equations in the next example are two equations that look different for the
same straight line.
Example 3
A system with infinitely many solutions
Solve the system by graphing:
2(y + 2) = x
x - 2y = 4
Solution
Write each equation in slope-intercept form:
| 2(x + 2) |
= x |
x - 2y |
= 4 |
| 2y + 4 |
= x |
-2y |
= -x + 4 |
| y |
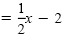 |
y |
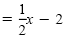 |
Because the equations have the same slope-intercept form, the original equations
are equivalent. Their graphs are the same straight line as shown in the
following figure.
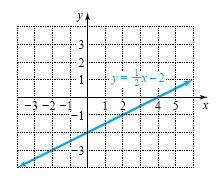
Every
point on the line satisfies both equations of the system. There are infinitely many
points in the solution set. The solution set is {(x, y)
| x - 2y = 4}.
|