Linear Systems of Equations with No Solution
A linear system has no solution if the graphs of the equations have no
points in common.
That is, if the lines are parallel and distinct, the linear system does not
have a solution.
Example 1
Graph each equation to find the solution of this system.
Solution
To graph each equation, first write it in slope-intercept form, y = mx + b.
• In slope-intercept form, the first equation is
The y-intercept is (0, -3). Plot (0, -3).
Use the slope,
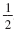, to plot a second point.
Draw the line through the two points.
• In slope-intercept form, the second equation is
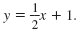
The y-intercept is (0, 1). Plot (0, 1).
Use the slope,
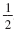, to plot a second point.
Draw the line through the two points.
The lines have the same slope,
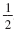, but different y-intercepts.
Therefore, the lines are distinct parallel lines.
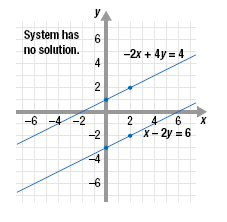
Since distinct parallel lines never intersect, this system has no solution.
A system that has no solution is called an
inconsistent system.
