Powers of a Monomial
What happens when a monomial is raised to a power? A good way
to introduce this concept is to work again with powers of 2.
First look at the squares of various powers of 2.
| 2
n |
( 2
n )2 |
| 2 1 = 2 |
4 = 2 2 |
| 2 2 = 4 |
16 = 2 4 |
| 2 3 = 8 |
64 = 2 6 |
| 2 4 = 16 |
256 = 2 8 |
| 2 5 = 32 |
1024 = 2 10 |
| 2 6 = 64 |
4096 = 2 12 |
Notice that when a power of 2 is squared, the exponent in the
result is doubled.
Example 1
Simplify ( x 4 ) 3.
Solution
To simplify the expression, write out the powers as products.
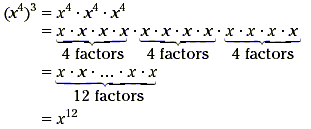
In this case, the exponent 4 is tripled. The exponent in the
final answer is 12, since the monomial is raised to the third
power. This works in general.
Power of a Power
When a power of a number or variable is raised to another
power, the result is that same number or variable whose exponent
is the product of the exponents.
( x m) n = x mn
Example 2
Simplify ( x 8 ) 7 .
Solution
( x 8 ) 7 = x 8 · 7 = x
56
Example 3
Simplify (15 3 ) 6 .
Solution
(15 3 ) 6 = 15 3 · 6 = 15
18
It is a good idea that you work out explicitly several
examples by expanding the powers into products, so that reasoning
behind the key idea is reinforced.
To understand this idea in the general case, take a look at
the following diagram.
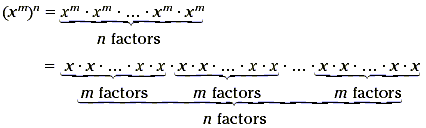
There are n groups of factors, each of which is itself a group
of m factors, so that there are mn factors all together. So, the
result is x mn .
You have now learned how to find powers of powers. Since
monomials are generally products of powers, it will be easy now
to learn how to find powers of products. This will be helpful in
finding powers of monomials.
How do you think te expression ( a · b ) 2 should
be simplified?
The following solution provides a good explanation.
| ( a · b ) 2 |
= ( a · b ) · ( a · b ) |
| |
= a · b · a · b |
| |
= a · a · b · b |
| |
= a 2 · b 2 |
This idea is shown below using numbers.
6 3 = 216
| 6 3 |
= (2 · 3) 3 |
| |
= 2 3 · 3 3 |
| |
= 8 · 27 |
| |
= 216 |
Power of a Product
A product raised to a power is the product of the factors
raised to the given power.
( a · b) m = a m · b m
A good way to show this is to use the following diagram.
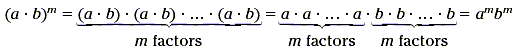
The middle expression, there are exactly m factors each of a
and b. Now let's combine these two ideas into one.
Power of a Monomial
For any whole numbers m, n, and p, ( a m · b
n) p = a mp b np.
Now you can evaluate powers and products of any monomials.
|