Dividing Rational Expressions
Dividing a - b by b - a
We can either factor b - a as -1(a - b) to get the common factor a - b, or
else use the fact that (a-b) ÷ (b-a) -1,
as shown in the next example.
Example 1
Dividing a - b by b - a
Find the product:
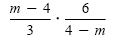
Solution
Instead of factoring out -1 from m - 4, we divide m - 4 by 4 - m to get -1:
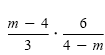 |
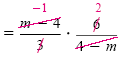 |
Note that (m - 4) ÷ (4 - m) = -1. |
| |
= -2 |
|
Dividing Rational Expressions
We divide rational numbers by multiplying by the reciprocal or multiplicative
inverse of the divisor. For example,
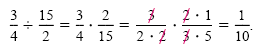
When we divide rational numbers, we use the following definition.
Division of Rational Numbers
If
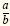 and and
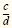 are rational numbers with are rational numbers with
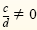 , then , then
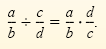
We use the same method to divide rational expressions: We invert the divisor
and multiply.
Example 2
Dividing rational expressions
Find each quotient.

Solution
a) The reciprocal of the divisor
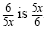 . .
b) The reciprocal of 4ab3c is
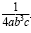
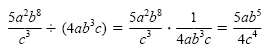 Quotient rule Quotient rule
|