Simplifying Complex Fractions
What do we mean by complex fractions?
Complex fractions are fractions whose numerator and/or
denominator themselves are expressions containing other
fractions.
Can a complex fraction become a simple fraction?
Yes, it can! The goal of simplifying complex fractions is to
rearrange them into equivalent simple fractions which are in
simplest form.
And can a simple fraction be simplified?
You should already know it can. The goal of simplifying a
simple fraction is to obtain an equivalent fraction that looks
simpler (i.e. it has less terms in its numerator and
denominator).
Sometimes the numerator and denominator of a complex fraction
are just single simple fractions themselves. Then, for the first
step in simplifying the complex fraction, we just use the
wellknown “invert and multiply” rule: multiply the
fraction in the numerator by the reciprocal of the fraction in
the denominator:
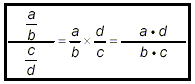
You see that the initial complex fraction on the left has been
turned into a single simple fraction on the right. This step is
justified only if the numerator and denominator of the original
complex fraction are both single simple fractions. When the
pattern in the box above is valid, all that is left to do in
simplifying the original complex fraction is to use methods
already illustrated many times in the last few documents in this
series to check whether the simple fraction on the right can be
simplified any further.
Example:
Simplify: 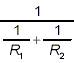
solution:
We include this simple example just to emphasize that you must
treat all complex fractions as complex fractions and apply the
general procedure illustrated in the previous examples whenever
you deal with a complex fraction.
(By the way, the subscript labels, 1 and 2, on the R’s
are just labels. In this case, consider R 1 and R
2 each to be distinct simple single literal symbols as a
whole, just as you might use the even simpler symbols such as x
and y to represent numerical values. In this instance, the
subscripts are used to distinguish the two symbols, and have no
deeper mathematical significance.)
This example seems very simple! Often people think: dividing
by a fraction means “invert and multiply,” and so here
we just do
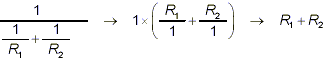
But as “natural” as this method appears to be here,
it is completely incorrect! To see this, just try a simple
numerical experiment with the initial and proposed final
simplified form. For instance, if R 1 = 2 and R 2
= 4, the original expression evaluates to
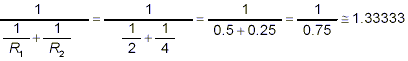
However, if we use the result of the erroneous “invert
and multiply” method shown above, we get
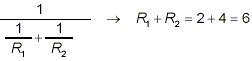
which is very different from the correct answer of 1.33333 (to
five decimal places).
The mistake above is that “invert and multiply”
applies only when the expression in the denominator is a single
simple fraction. Here, our denominator is a sum of two simple
fractions. So, following the general strategy for simplifying
complex fractions, we must first reorganize the expression in the
denominator into a simple fraction.
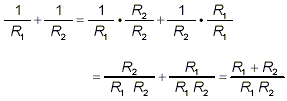
So now,
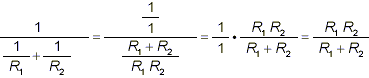
as the correct simplification of the original complex
fraction.
By the way, the little numerical experiment that demonstrated
the presence of error in the incorrect approach earlier works
fine here. Substituting R 1 = 2 and R 2 = 4
in the final expression just above gives
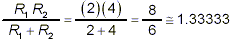
which we know is the value we should expect to get. (This
numerical experiment is not a proof that our final result is
correct, since it might be that the final result gives the same
value as the original complex fraction for these values of R
1 and R 2 just by coincidence. The equivalence
of two mathematical expressions cannot be “proven” with
a single numerical experiment – certainty that a result is
correct requires careful checking of the algebraic connection
between the two expressions. However, if two expressions do not
give the same numerical result when the same values are
substituted for the literal symbols they contain, that is certain
proof that they are not equivalent mathematical expressions.)
You might be wondering: why spend all this time learning how
to simplify complex fractions? Surely such strange expressions
are found only in math books and would never be encountered in
actual technical applications!
But this is not so. Recall that a fraction is one way of
writing the division of one mathematical expression by another
mathematical expression. Whenever either or both of the
expressions involved in such a division operation also contain
fractions themselves, then writing the division as a fraction
generates a complex fraction. Since division is a very common
mathematical operation in all technical applications, complex
fractions are not uncommon in the analysis of actual technical
problems. (For instance, the complex fraction considered in
Example above arises in describing one of the very simplest types
of electrical circuits.)
And, since complex fractions are “complex,” there is
value in being able to simplify them to make their use in
subsequent steps of the problem solving process that much easier.
|