Real Numbers and Notation
Real Numbers
People first used numbers to count things, such as sheep in a flock or
members of a family. Numbers such as 1, 2, 3, 28, and 637 are called counting numbers.
The counting numbers are an example of a set. A set is a collection of
distinct numbers, objects, etc., called the elements or members of the set.
The elements are often enclosed in braces, {}.
For example, the set with elements 4, 12, and 20 can be written like this:
{4, 12, 20 }
Using this notation, we can indicate the set of counting numbers like this:
{1, 2, 3, 4, … }
The ellipsis (the three dots …) shows that the counting numbers continue
in this pattern.
People soon discovered that they needed other kinds of numbers to deal
with the increasing complexity of their world. So, they developed the
following additional sets of numbers:
The natural numbers is another name for the counting numbers:
{1, 2, 3, 4, …}
The whole numbers are the counting numbers along with 0:
{0, 1, 2, 3, 4, ...}
The integers are the whole numbers and their opposites:
{…, -3, -2, -1, 0, 1, 2, 3, …}
The rational numbers are numbers that can be written in the form
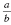 , where a and b are integers and b is not 0. , where a and b are integers and b is not 0.
The following set contains five rational numbers:
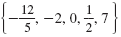
The irrational numbers are numbers that cannot be written in the
form
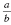 . The following set contains three irrational numbers. . The following set contains three irrational numbers.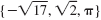
The real numbers are the rational numbers and the irrational numbers
combined. So, the real numbers include the natural numbers, whole
numbers, integers, rational numbers, and irrational numbers.
The following set contains eight real numbers.
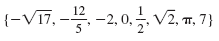
Integers such as -2, 0, and 7 are rational
numbers because they can be written in the
form
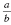 where b
≠ 0: where b
≠ 0:
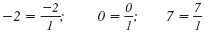
Terminating decimals such as 0.75, and
1.375 are rational numbers because they
can be written in the form
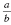 where b
≠ 0: where b
≠ 0:

Repeating decimals such as 0.5555… and
0.121212… are rational numbers because
they can be written in the form
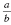 , where
b ≠ 0: , where
b ≠ 0:
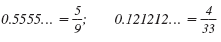
An irrational number such as
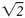 can be approximated as a decimal, but the digits
do not terminate and do not repeat in a
pattern. For example: can be approximated as a decimal, but the digits
do not terminate and do not repeat in a
pattern. For example:
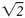 is approximately 1.41421356237 is approximately 1.41421356237
Example 1
For each number, list the sets to which the number belongs.
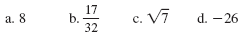
Solution
a. 8 is a natural number, an integer, a rational number
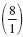 , and a real
number. , and a real
number.
b.
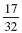 is a rational number and a real number. is a rational number and a real number.
c.
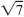 is an irrational number and a real number. is an irrational number and a real number.
d. -26 is an integer, a rational number
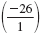 , and a real number. , and a real number.
|