Graphing Technology: Parent and Family Graphs

Objective Use a graphing calculator to explore how changing the values of m and b affect the graph of y = mx + b .

In this lesson, you will be asked to explore the graphs of linear equations, and how they depend on the slope and the y-intercept. There are several main ideas that this lesson reinforces.

Key Ideas

• Lines with positive slope have the property that as we move to the right along the line, the line slopes upward.

• Lines with negative slope slope downward.

• Lines with zero slope are horizontal.

• Lines with greater positive slope move upward more steeply. Lines with lesser negative slope move downward more steeply.

Try to explore both positive and negative values of m by graphing equations of the form y = mx . The collection of lines obtained in this way can be thought of as a family of lines. A family of lines is shown below.

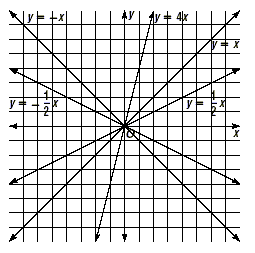
Any one of the lines in the family can be thought of as a parent, since the other members of the family are obtained by rotating that line. Typically a simple member, such as y = x , is the parent graph.

 

Key Idea

In graphing an equation of the form y = mx + b ,

• the line shifts up as the value of b increases, and

• the line shifts down as the value of b decreases.

Try to explore by graphing equations of the form y = x + b for various values of b, both positive and negative. The lines are simply a family of parallel lines that move up or down. Again, a simple member, such as y = x , is the parent graph. A family of graphs is shown below.

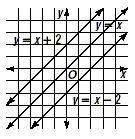
Next, try to explore the following different families of lines, y = 2x + b and y = -x + b , for various values of b. You will again find families of parallel lines, with slopes 2 and -1, respectively.

“What can you say about lines having the same slope?”

The answer to this question is that they are parallel.