Solving Equations with Radicals and Exponents
One of our goals in algebra is to keep increasing our knowledge of solving equations
because the solutions to equations can give us the answers to various applied
questions. In this section we will apply our knowledge of radicals and exponents to
solving some new types of equations.
The Odd-Root Property
Because (-2)3 = -8 and 23 = 8, the equation x3
= 8 is equivalent to x = 2. The
equation x3 = -8 is equivalent to x = -2. Because there is only one real odd root
of each real number, there is a simple rule for writing an equivalent equation in this
situation.
Odd-Root Property
If n is an odd positive integer,
xn = k is equivalent to
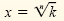 for any real number k.
Example 1
Using the odd-root property
Solve each equation.
a) x3 = 27
b) x5 + 32 = 0
c) (x - 2)3 = 24
Solution
| a) x3 |
= 27 |
|
| x |
 |
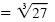Odd-root property |
| x |
= 3 |
|
Check 3 in the original equation. The solution set is {3}.
| b) x5 + 32 |
= 0 |
|
| x5 |
= -32 |
Isolate the variable. |
| x |
 |
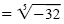Odd-root property |
| x |
= -2 |
|
Check -2 in the original equation. The solution set is {-2}.
| c) (x - 2)3 |
= 24 |
Odd-root property |
| x + 2 |
 |
 |
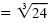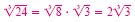| x |
=
 |
|
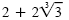Check. The solution set is {
 }.
|
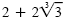