Multiplying Fractions
What is 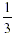 of of 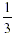 ? ?
We know that 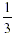 of (a) of (a) 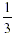 is is 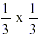 ("of" = "times"). ("of" = "times").
The rule for multiplying fractions is:
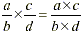
which means that 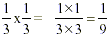 . But where does this rule come from? . But where does this rule come from?
Let us apply this rule using the example of the cake:
Think of a piece that is one third (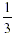 ) )
of the cake, i.e. which fits into the whole cake 3 times. Now
visualize a slice which is one third of the above piece. Clearly
this will fit 9 times into the whole cake, i.e. it is 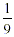 of the cake. This slice is of the cake. This slice is 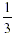 of of 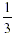 the same as the same as 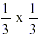 . .
So we have established why 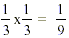 which is the same as which is the same as 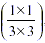 , as in the rule given above. , as in the rule given above.
Had we started with a fifth (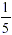 ) of the cake, and then taken a slice one third of
that fifth, clearly 15 such slices would have fitted into the
whole cake, i.e. this slice would be one 15th of the cake (which
we can write as ) of the cake, and then taken a slice one third of
that fifth, clearly 15 such slices would have fitted into the
whole cake, i.e. this slice would be one 15th of the cake (which
we can write as 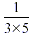 , because the 15, of course, came from the
3 × 5. , because the 15, of course, came from the
3 × 5.
So we have established that 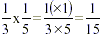 (again as in the rule). Now, had we started with (again as in the rule). Now, had we started with 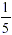 of seven cakes (rather than of 1), i.e. of seven cakes (rather than of 1), i.e. 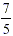 , and then went on, as before, taking one third of
the this, then the final piece would have been 7 times bigger
(than the above , and then went on, as before, taking one third of
the this, then the final piece would have been 7 times bigger
(than the above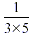 ), namely, ), namely, 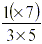 . .
Finally, for the 'sub-division' of the cake, had we taken two
thirds (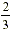 ), rather than one third, the result would
be yet another 2 times bigger, i.e. ), rather than one third, the result would
be yet another 2 times bigger, i.e. 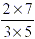 . .
So, we have shown why 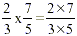 , thus showing where the general rule , thus showing where the general rule
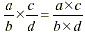 comes from. comes from.
|