Circumference and Area of Circles
Understanding Circles
A circle is named by the point in the center.
The distance around a circle is called the circumference.
Any segment from the center to the circumference is called the radius.
Any segment connecting two points on the circle is called a chord.
A chord through the center is called the diameter.
The part of the circumference between two points called an arc.
An arc contains the same number of degrees as its central angle.
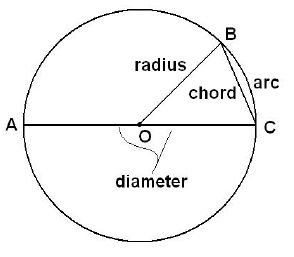
This is circle O with radius OB,
diameter AC,
chord BC,
central angle BOC and arc BC.
Computing Circumferences
Let’s look at how the diameter is related to circumference.
The ancient Greek mathematicians found that the
circumference divided by the diameter of a circle is always the same. Regardless of the size of
the circle, there is a constant ratio of diameter to circumference. They named this number with
the Greek letter pi, π.
For a long time they thought the value of pi was 22/7, but later found p could not be
represented as a simple ratio of any two integers. Since it can’t be written as a ratio, we call pi
an irrational number.
The precise value of p can be determined by adding an infinite series of continually decreasing
fractions. It must therefore have an infinitely long series of decimal digits that never repeat.
Circumference = pi times diameter
C = π d
π is approximately = 3.1415926535…
Does this mean π is infinitely large? No, it is always greater than two and less
than four. But it does take an infinite series of digits to write.
We often write answers involving π as just some number times the symbol
π. This gives people
an ‘exact’ answer with a satisfying feel. Otherwise you don’t know how many digits are
significant, or where to round the answer. Since p goes on forever, to be really precise you
would need to write billions of digits.
By the way: “Ten decimals of π are sufficient to give the circumference of the earth to the
fraction of an inch, and thirty decimals would give the circumference of the whole visible
universe to a quantity imperceptible with the most powerful microscope.†– Simon Newcomb
Example:
How much smaller is the circumference of the inner circle than that of the outer
circle?
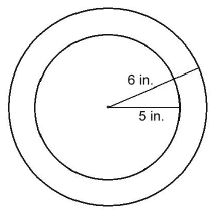
Cinner = 2 × 5 × π = 10π
Couter = 2 × 6
× π = 12π
Couter - Cinner = 12π - 10π
= 2π
= about 6.28 inches
|