Percents

Like fractions and decimals, percents are a way of representing part of something.

Why do we use percentages? It is a simple and convenient way to use ratios. It is easier to say “five percent” than “zero point zero five of the total”.

You can use percents anywhere ratios are used, and that’s just about everywhere! Here are some examples…

Percents can compare groups.

Percents can predict the future.

Percents can simplify many numbers.

Percents are particularly useful with money.

 

Percent

Percent or % is a special ratio that means a number of parts “per one hundred”. It is a standard of measure.

Examples:

10% may be written as

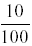
25% may also be written as

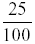
99% is written as

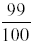
125% may be written as

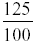
Definitions:

Base - is the whole quantity

Percentage - is the portion of the whole quantity

Rate - is the percent (%), think of “ratio” when you see this!

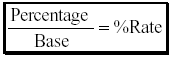
Percents may be added, subtracted, multiplied or divided in the same way as other ratios.

Example: 8% + 6% = 14%

Example: 18% - 12% = 6%

Example: 18% ÷ 9 = 2%

Example:  7% × 5 = 35%

 

Converting percents to decimals

To change a percent to a decimal, remove the percent sign and move the decimal point two places to the left (divide by 100).

Example: Change 25% to a decimal

 

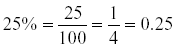
Example: Change 200% to a decimal

 

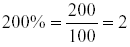
Converting decimals to percents

To change a decimal to a percent, multiply by 100 (move the decimal point two places to the right) and write the percent sign:

Example: Change 0.057 to a percent

0.057 = 5.7 %

Example: Change 2.43 to a percent

2.43 = 243%

 

Computing percentages and percents

Example: What is 8% of 50 ?

Solution: The rate or percent is 8%. The base or whole quantity is 50. Remember that a “percent” is the same as a ratio. Also recall that “of” is the same as multiplying. First, convert the percent to a decimal:

8% = 0.08

Next, multiply the decimal by the base:

50 × 0.08 = 4

Answer: 8% of 50 is 4

Example: 25 is what percent of 50?

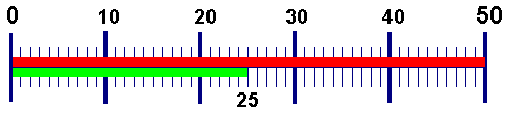
Solution: To solve a “what percent” problem, we must find the ratio.

Here the base or whole quantity is again 50.

The percent or part of the whole quantity is 25.

To solve for the percent, divide the percent 25 by the base 50.

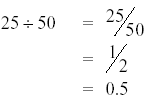
Now convert the decimal fraction 0.5 into percent by multiplying by 100 and writing %: