Writing Linear Equations in Slope-Intercept Form
Slope-Intercept Form
The slope-intercept form is a special case of the point-slope
form. The given point of the line (x 0 , y 0
) lies on the y-axis, so x0 = 0. This means that the
equation is of the form y - y 0 = mx, or y = mx + y
0 . The equation is therefore given explicitly when both
the y-intercept and the slope are known, and is simpler than the
more general point-slope form. This is perhaps the most common
and most important normal form for the equation of a line.
Example 1
Write the slope-intercept form of the equation for a line that
goes through (0, 4) and has a slope of 5.
Solution
| y - y 0 |
= m ( x - x 0 ) |
Point-slope form |
| y - 4 |
= 5x |
Replace x 0 with 0, y 0
with 4, and m with 5. |
Now add 4 to each side of this equation in order to express y
in terms of x . The result is the following equation.
y = 5 x + 4
Point out that 5 is the slope of the line and that 4 is the
y-intercept.
Example 2
Write the slope-intercept form of the equation for a line that
goes through (0, -3) and has a slope of -1.
Solution
| y - y 0 |
= m ( x - x 0 ) |
Point-slope form |
| y - ( -3) |
= ( -1)x |
Replace x 0 with 0, y 0
with -3 , and m with -1. |
| y + 3 |
= -x |
|
Now subtract 3 from each side of this equation in order to
express y in terms of x . The result is the following equation.
y = -x - 3
Point out that -1 is the slope of the line and that -3 is the
y -intercept.
Notice that these equations are really much simpler than the
general point-slope form, since there are fewer terms. Also note
that in each case, the coefficient of x is the slope and the
constant term is the y-intercept.
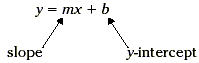
Key Idea An equation for a line is in
slope-intercept form if it is of the form y = mx + b, where m is
the slope of the line and b is the y-intercept.
Any line that is not vertical has an equation that is in
slope-intercept form. A vertical line could not possibly have an
equation in slopeintercept form, for the same reason that it
cannot have an equation in point-slope form - the slope is
undefined.
|