Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Linear Equations

Slope

Definition of Slope	The steepness of a line in the coordinate plane is called its slope. It is defined as the ratio of the rise, or vertical change in y, to the run, or horizontal change as you move from one point to the other.
Determining Slope Given Two Points	Given the coordinates of two points, ( x₁, y₁) and ( x₂, y₂), on a line, the slope m of the line can be found as follows.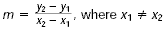

Example

What is the slope of the line that passes through (4, -6) and (-2, 3)?

Solution

Let x₁ = 4, y₁= -6, x₂= -2, and y₂= 3.

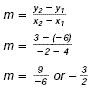
Writing Linear Equations in Point-Slope and Standard Forms

Point-Slope Form of a Linear Equation	For a given point ( x₁, y₁) on a nonvertical line having slope of m, the point-slope form a linear equation is as follows: y - y₁= m( x - x₁). The linear equation of a vertical line, which has an undefined slope, through a point ( x₁, y₁) is x = x₁.
Standard Form	The standard form of a linear equation is Ax + By = C, where A, B, and C are integers, A 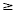0, and A and B are not both zero.

Example

Write the equation, first in point-slope form and then in standard form, of the line that passes through (2, 3) and has a slope of 5.

Solution

Point Slope Form	y - y₁= m( x - x₁)
	y - 3 = 5( x - 2)
y - 3 = 5x - 10	Distribute.
5x - 10 = y - 3	Reflexive Property ( = )
5x - y = 7	Add 10 and subtract y from each side.
Standard Form:	5x - y = 7, where A = 5, B = -1 and C = 7

Writing Linear Equations in Slope-Intercept Form

The coordinates at which a graph intersects the axes are known as the x-intercept and the y-intercept.

Finding Intercepts	To find the x-intercept, substitute 0 for y in the equation and solve for x. To find the y-intercept, substitute 0 for x in the equation and solve for y.
Slope-Intercept Form of a Linear Equation	If a line has a slope of m and a y-intercept of b, then the slope-intercept form of an equation of the line is y = mx + b.

Example

Find the x - and y -intercepts of the graph of 2x + 3y = 5. Then, write the equation in slope-intercept form.

Solution

2x + 3(0) = 5	Let y = 0	2(0) + 3y = 5	Let x = 0
2x = 5		3y = 5
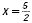	The x-intercept is	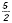	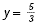The y-intercept is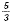
Slope-Intercept form: 2x + 3y = 5