Quadratic Equations
Example 1
The solutions of a quadratic equation are 4 and -1. Use their sum and
product to find a quadratic equation with those solutions.
Solution
For a quadratic equation, ax2 + bx + c = 0, the sum of the solutions is
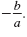
The sum of the given solutions is
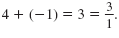
We have
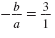
So, if a = 1, then b = -3.
The product of the solutions is
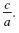
The product of the given solutions is
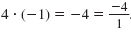
We have
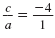
So, if a = 1, then c = -4.
| For the quadratic equation, ax2 + bx + c = 0, let a
= 1, b = -3, and c = -4.
|
ax2 + bx + c
= 0 |
| Substitute these values in the equation.
Simplify. |
1x2 + (-3)x - 4 = 0
x2 - 3x - 4 = 0 |
The equation, x2 - 3x - 4 = 0 is a quadratic equation
with solutions 4 and -1.Note:
x2 - 3x - 4 = 0
Any nonzero multiple of this equation
also has solutions 4 and -1.
Here are some examples:
2x2 - 6x - 8 = 0
3x2 - 9x - 12 = 0
Example 2
The quadratic equation 2x2 - 7x + c = 0 has discriminant 9.
What are the solutions of the equation?
Solution
First, we’ll find the value of c. Then we’ll solve the equation.
To find c, we use the discriminant, b2 - 4ac. For the given equation, a
= 2 and b = -7.
We also know the discriminant is 9.
Substitute a = 2 and b = -7.
Simplify.
Subtract 49 from both sides. Divide both sides by -8.
Now we know that c = 5. |
b2 - 4ac = 9
(-7)2 - 4(2)c = 9
49 - 8c = 9
-8c = -40 c = 5 |
| We use the quadratic formula to solve
the equation 2x2 - 7x + c = 0. |
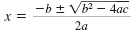 |
| Substitute a = 2, b = -7, and c = 5. |
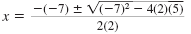 |
| Simplify.
|
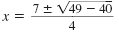 |
| Simplify the radicand.
|
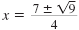 |
| Simplify the square root.
|
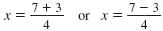 |
| Simplify. |
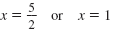 |
Thus, if the discriminant of 2x2 - 7x + c = 0 is 9,
the solutions of the equation are
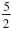 and 1. and 1.
|