Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Proportions

An equation that expresses the equality of two rational expressions is called a proportion. The equation

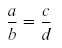
is a proportion. The terms in the position of b and c are called the means. The terms in the position of a and d are called the extremes. If we multiply this proportion by the LCD, bd, we get

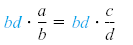or ad = bc.

The equation ad = bc says that the product of the extremes is equal to the product of the means. When solving a proportion, we can omit multiplication by the LCD and just remember the result, ad = bc, as the extremes-means property.

Extremes-Means Property

If 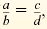then ad = bc.

The extremes-means property makes it easier to solve proportions.

Example 1

A proportion with one solution

Solve

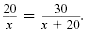
Solution

Rather than multiplying by the LCD, we use the extremes-means property to eliminate the denominators:

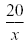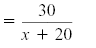20(x + 20)

= 30x

Extremes-means property

20x + 400

400

= 30x

= 10x

= x

Check 40 in the original equation. The solution set is {40}.

Example 2

A proportion with two solutions

Solve

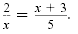
Solution

Use the extremes-means property to write an equivalent equation:

x(x + 3)			= 2 Â· 5	Extremes-means property
x² + 3x			= 10
x² + 3x - 10			= 0
(x + 5)(x - 2)			= 0	Factor.
x + 5 = 0	or	x - 2	= 0	Zero factor property
x = -5	or	x	= 2

Both -5 and 2 satisfy the original equation. The solution set is {-5, 2}.

Caution

Use the extremes-means property only when solving a proportion. It cannot be used on an equation such as

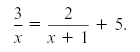
Helpful hint

The extremes-means property is often referred to as cross multiplying. Whatever you call it, remember that it is nothing new. You can accomplish the same thing by multiplying each side of the equation by the LCD.

Example 3

Ratios and proportions

The ratio of men to women at a football game was 4 to 3. If there were 12,000 more men than women in attendance, then how many men and how many women were in attendance?

Solution

Let x represent the number of men in attendance and x - 12,000 represent the number of women in attendance. Because the ratio of men to women was 4 to 3, we can write the following proportion:

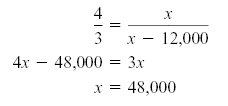
So there were 48,000 men and 36,000 women at the game.