Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Synthetic Division

When dividing a polynomial by a binomial of the form x c, we can use synthetic division to speed up the process. For synthetic division we write only the essential parts of ordinary division. For example, to divide x³ - 5x² + 4x - 3 by x - 2, we write only the coefficients of the dividend 1, -5, 4, and -3 in order of descending exponents. From the divisor x - 2 we use 2 and start with the following arrangement:

1 - 5 4 - 3

(1 Â· x³ - 5x² + 4x - 3) Ã· (x - 2)

Next we bring the first coefficient, 1, straight down:

2	1 ↓	-5 4 -3 Bring down
	1

We then multiply the 1 by the 2 from the divisor, place the answer under the -5, and then add that column. Using 2 for x - 2 allows us to add the column rather than subtract as in ordinary division:

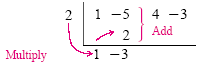
We then repeat the multiply-and-add step for each of the remaining columns:

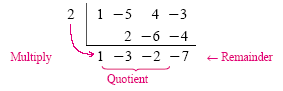
From the bottom row we can read the quotient and remainder. Since the degree of the quotient is one less than the degree of the dividend, the quotient is 1x² - 3x - 2. The remainder is -7.

The strategy for getting the quotient Q(x) and remainder R by synthetic division can be stated as follows.

Strategy for Using Synthetic Division

1. List the coefficients of the polynomial (the dividend).

2. Be sure to include zeros for any missing terms in the dividend.

3. For dividing by x c, place c to the left.

4. Bring the first coefficient down.

5. Multiply by c and add for each column.

6. Read Q(x) and R from the bottom row.

Caution

Synthetic division is used only for dividing a polynomial by the binomial x - c, where c is a constant. If the binomial is x - 7, then c = 7. For the binomial x + 7 we have x + 7 = x - (- 7) and c = - 7.

Example

Using synthetic division

Find the quotient and remainder when 2x⁴ - 5x² + 6x - 9 is divided by x + 2.

Solution

Since x + 2 = x - (-2), we use 2 for the divisor. Because x³ is missing in the dividend, use a zero for the coefficient of x³:

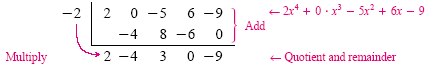
Because the degree of the dividend is 4, the degree of the quotient is 3. The quotient is 2x³ - 4x² + 3x, and the remainder is -9. We can also express the results of this division in the form quotient :

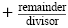2x⁴ - 5x²+ 6x - 9	= 2x³ - 4x² + 3x +	-9
x + 2		x + 2