Dividing Monomials
After studying this lesson, you will be able to:
- Divide monomials.
- Simplify expressions with negative exponents.
Dividing Powers with the Same Base: The base
stays the same; Subtract the exponents
After subtracting the exponents, you will put the remaining
exponent where the largest exponent was to begin with. For
example, if you have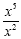 
which is a division problem, we will subtract the exponents 5 -2
which gives us 3. We will be left with x 3 . We leave
this in the numerator, since the largest exponent was in the
numerator to begin with.
Zero Power Rule: Any non-zero number raised
to the zero power is one.
Example 1
a 0 = 1
Example 2
x 0 = 1
Example 3
3 0 = 1
Example 4
-6 0 = 1
Negative Exponents
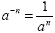
When we are working with negative exponents, we usually try to
convert them to positive exponents. We can change negative
exponents to positive exponents by "moving them up or
down". For example, if we have x -3 , we can make
the -3 positive by moving it from the top (numerator) to the
bottom (denominator). We can then rewrite x -3 as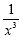 
. Notice that we moved the negative exponent to the denominator.
We put the 1 in the numerator to hold the place. Remember, we
cannot leave a numerator empty.
Example 5
Rewrite using positive exponents: y -4
To make the negative exponent positive, we "move"
it. Since it is in the numerator, we move it to the denominator.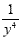 
Remember to put a 1 in the numerator to hold the place.
Example 6
Rewrite using positive exponents: 10 -2
To make the negative exponent positive, we "move"
it. Since it is in the numerator, we move it to the denominator.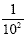 
Remember to put a 1 in the numerator to hold the place. This
expression will simplify. 10 2 = 100 so we can
simplify to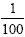 
?
Example 7
Rewrite using positive exponents: 6 -3 To make the
negative exponent positive, we "move" it. Since it is
in the numerator, we move it to the denominator.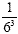 
Remember to put a 1 in the numerator to hold the place.
This expression will simplify. 6 3 = 216 so we can
simplify to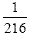 
Example 8
Simplify. Use only positive exponents:
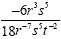
The first thing we need to do is to simplify the -6 and the
18. We reduce to -1 and 3 to give us:
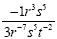
Now, we need to convert the negative exponents to positive
exponents. We do so by "moving" the negative exponents.
We first move the r -7 to the top. Since we already
have r 3 on the top, we will now have r 7 r
3 which simplifies to r 10
We have s 5 on the top and bottom, so those cancel
each other out. Now we have this:
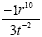
The last thing we need to do is to move t -2 to the
top so that the exponent will be positive. This will give us the
final answer:
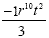
Example 9
Simplify. Use only positive exponents:
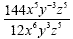
The first thing we need to do is to simplify the 144 and the
12. We reduce to 12 and 1 to give us:
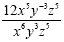
Since we have x 5 on top and x 6 on
bottom, we subtract the exponents. (Both of these are positive so
we don't move them.) Simplifying will give us x on the bottom.
(We subtract 5 from 6. We put the x on bottom because the larger
exponent was on the bottom.) Now, we need to convert the negative
exponents to positive exponents. We do so by "moving"
the negative exponents. We first move the y -3 to the
bottom. Since we already have y 3 on the bottom, we
will now have y 3 y 3 which simplifies to y
6 We have z 5 on the top and bottom, so those
cancel each other out.
Now we have the answer: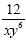 
