Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Division and Factoring

To factor a polynomial means to write it as a product of two or more simpler polynomials. If we divide two polynomials and get 0 remainder, then we can write

dividend = (divisor)(quotient)

and we have factored the dividend. The dividend factors as the divisor times the quotient if and only if the remainder is 0. We can use division to help us discover factors of polynomials. To use this idea, however, we must know a factor or a possible factor to use as the divisor.

Example 1

Using synthetic division to determine factors

Is x - 1 a factor of 6x³ - 5x² - 4x + 3?

Solution

We can use synthetic division to divide 6x³ - 5x² - 4x + 3 by x - 1:

1	6	-5	-4	3
	↓	6	1	-3
	6	1	-3	0

Because the remainder is 0, x - 1 is a factor, and

6x³ - 5x² - 4x + 3 = (x - 1)(6x² + x - 3).

Example 2

Using division to determine factors

Is a - b a factor of a³ - b³?

Solution

Divide a³ - b³by a - b. Insert zeros for the missing a²b- and ab²-terms.

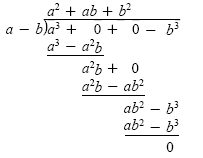
Because the remainder is 0, a - b is a factor, and

a³ - b³ = (a - b)(a² + ab + b²).