Simplifying Sums and Differences of Square Roots
Sums and differences of square roots are often fairly ugly
expressions to deal with algebraically, but sometimes we can use
the methods for simplification of single square roots to help get
lengthier expressions with two or more square root terms into a
more compact form. To illustrate ways to simplify a sum or
difference of terms containing square roots, consider the
following very simple example:
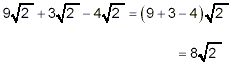
The grouping together of the coefficients 9, 3, -4, in
brackets as shown above makes use of the distributive law for
multiplication, which we described earlier in these notes in the
discussion of the use of brackets.
Alternatively, you could regard
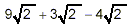
as saying: “we have 9 of these 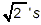 , and another 3 of these , and another 3 of these
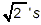 , and we’ve taken
away 4 of these , and we’ve taken
away 4 of these 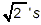 . That means we have, on
balance, (9 + 3 – 4) = 8 of these . That means we have, on
balance, (9 + 3 – 4) = 8 of these 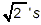 left.” But “8
of these left.” But “8
of these 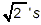 ” is written
mathematically as ” is written
mathematically as 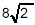 .
(Substitute the word “banana” for the symbol .
(Substitute the word “banana” for the symbol 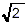 in the sentences above
if you’re having trouble understanding the logic of this
method.) We can regard this method as collecting together all
terms which have identical square root parts. in the sentences above
if you’re having trouble understanding the logic of this
method.) We can regard this method as collecting together all
terms which have identical square root parts.
Now, when the expression involves square roots of different
numbers, we first need to simplify each square root as much as
possible before collecting the terms with identical square root
parts.
Example:
Simplify 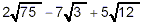
solution:
We first check the square roots in each of the three terms to
see if any of them by themselves can be simplified:
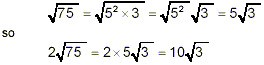
Then
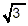 is as simple as
possible. is as simple as
possible.
Finally,
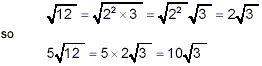
Thus, our original expression becomes
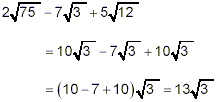
This is its simplest form.
Example:
Simplify 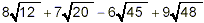
solution:
Once again, we first simplify each square root part as much as
possible:
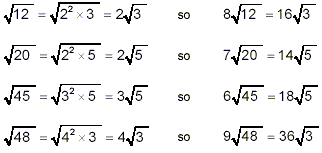
Thus
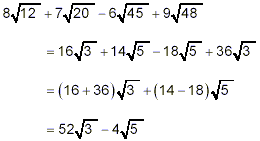
This is as simple as we can get the original expression
because there is no simple way to combine terms involving 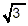 with terms involving with terms involving 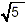 . .
|