Using the “FOIL†Method to Multiply Two Binomials
To multiply a binomial by a binomial, we use the Distributive Property
twice.
For example, let’s multiply (a + b)(c + d).
| Distribute (c + d) to both a and b. |
(a + b)(c + d) = a(c + d) + b(c + d) |
| Distribute both a and b to
each term in (c + d). |
= ac + ad + bc + bd |
Notice that each term in (a + b) has been
multiplied by each term in (c + d).
To remember how to multiply two binomials, we use the word FOIL.
FOIL stands for First, Outer, Inner, Last.
• The product of the First terms is ac.
• The product of the Outer terms is ad.
• The product of the Inner terms is bc.
• The product of the Last terms is bd.
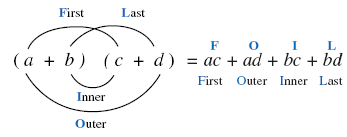
Note:
This picture may help you remember how
to use the FOIL method. The arcs form a
“face.â€

Example 1
Find: (x - 2)(x + 5)
| Solution |
|
F |
|
O |
|
I |
|
L |
| Use FOIL. Simplify each product.
Combine like terms. |
(x - 2)(x + 5) = =
= |
(x)(x) x2
x2 |
+ +
+ |
(x)(5) 5x
|
+ -
3x |
(-2)(x) 2x
|
+ -
- |
(-2)(5) 10
10 |
So, (x - 2)(x + 5) = x2 + 3x - 10.
Example 2
Find: (3w - 7)(9w - 5)
| Solution |
|
F |
|
O |
|
I |
|
L |
| Use FOIL. Simplify each product. Combine like terms. |
(3w - 7)(9w - 5) = =
= |
(3w)(9w) 27w2
27w2 |
+ -
- |
(3w)(-5) 15w
|
+ -
78w |
(-7)(9w) 63w
|
+ +
+ |
(-7)(-5) 35
35 |
So, (3w - 7)(9w - 5) = 27w2 - 78w + 35.
|