Solving Linear Equations
To solve some equations, we must simplify the equation before using the
properties of equality.
Example 1
Simplifying the equations first
Solve the equation 2(x - 4) + 5x = 34.
Solution
Before using the properties of equality, we simplify the expression on the
left-hand side of the equation:
| 2(x - 4) + 5x |
= 34 |
|
| 2x - 8 + 5x |
= 34 |
Distributive property |
| 7x - 8 |
= 34 |
Combine like terms. |
| 7x - 8 + 8 |
= 34 + 8 |
Add 8 to each side. |
| 7x |
= 42 |
Simplify. |
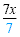 |
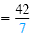 |
Divide each side by 7 to get a single x on the left side.
|
| x |
= 6 |
|
To check, we replace x by 6 in the original equation and simplify:
| 2(6 - 4) + 5 · 6 |
= 34 |
| 2(2) + 30 |
= 34 |
| 34 |
= 34 |
The solution se to the equation is {6}.
|