Solving Nonlinear Equations by Factoring
Example
Solve for x: x 3 + 2x = 6
+ 3x 2
| Solution Step 1 Write the equation in standard form.
Subtract 6 and 3x2 from both sides.
|
x3 + 2x
x3 - 3x2 +
2x - 6 |
=
6 + 3x2 = 0 |
|
Step 2 Factor by grouping.
Factor out the common factor, (x - 3). Step 3 Use the Zero Product Property. |
x2(x
- 3) + 2(x - 3) (x - 3)(x2
+ 2)
x - 3 = 0 or x2 + 2 |
= 0 = 0
= 0 |
Step 4 Solve for the variable.
|
x = 3 or x2 |
= -2 |
|
Take the square root of each side.
|
x |
 |
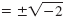Write
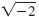 as an imaginary number. |
x |
 |
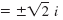So, the three solutions are x = 3,
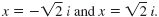
Note:
Recall that a negative number under a
square root results in an imaginary
number, which we indicate by using the
letter i. Thus,
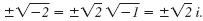
The equation x 3 + 2x = 6
+ 3x 2 written in standard form is x 3 - 3x 2 +
2x - 6 = 0. The graph of the corresponding function,
f(x) = x 3 - 3x 2 +
2x - 6 is shown.
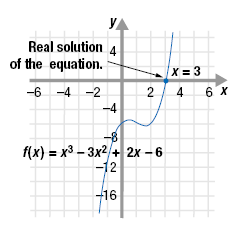
The graph crosses the x-axis at only one location, x = 3. This is because
the only real number solution is x = 3. In a Cartesian coordinate system,
the x- and y- axes represent real numbers. Therefore, the imaginary
solutions do not appear on the graph. However, the imaginary solutions
check in the original equation.
|
