Properties of Rational Expressions
A ratio of two integers is called a rational number; a ratio of two polynomials is
called a rational expression. Rational expressions are as fundamental to algebra as
rational numbers are to arithmetic. In this section we look carefully at some of the
properties of rational numbers and see how they extend to rational expressions.
Definition of Rational Expressions
A rational expression is the ratio of two polynomials with the denominator not
equal to zero. For example,
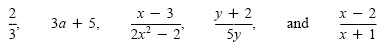
are rational expressions. The rational number
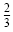 is a rational expression because 2
and 3 are monomials and is a rational expression because 2
and 3 are monomials and
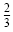 is a ratio of two monomials. If the denominator of a
rational expression is 1, it is usually omitted, as in the expression 3a + 5. is a ratio of two monomials. If the denominator of a
rational expression is 1, it is usually omitted, as in the expression 3a + 5.
Domain
The domain of a rational expression is the set of all real numbers that can be used
in place of the variable. Because the denominator of a rational expression cannot
be zero, the domain of a rational expression consists of the set of real numbers
except those that cause the denominator to be zero. The domain of
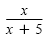
is the set of all real numbers excluding -5. In set-builder notation this set is
written as
{x | x ≠
-5}, and in interval notation it is written as
(-∞, -5) È (-5,
∞).
Helpful hint
If the domain consists of all
real numbers except -5,
some people write R - {-5} for the domain. Even though
there are several ways to indicate
the domain, you should
keep practicing interval notation
because it is used in
algebra, trigonometry, and
calculus.
Example 1
Domain
Find the domain of each rational expression.

Solution
a) The denominator is zero if x + 9 = 0 or x = -9. The domain is {x
| x ≠
-9} or
(-∞, -9) È (-9,
∞).
b) The denominator is zero if 5y = 0 or y = 0. The domain is {y
| y ≠ 0} or
(-∞, 0) È (0,
∞).
c) The denominator is zero if 2x2 - 2 = 0. Solve this equation.
| |
2x2 - 2 = 0 |
|
|
| |
2(x2 - 1) = 0 |
|
Factor out 2. |
| |
2(x + 1)(x - 1) = 0 |
|
Factor completely. |
| x + 1 = 0 |
or |
x - 1 = 0 |
|
Zero factor property |
| x = -1 |
or |
x = 1 |
|
|
The domain is the set of all real numbers except -1 and 1. This set is written as
{x | x ≠
-1 and x ≠ 1}, or in interval notation as
(-∞, �1) È (-1, 1)
È (1, ∞).
Caution
The numbers that you find when you set the denominator
equal to zero and solve for x are not in the domain of the rational expression. The
solutions to that equation are excluded from the domain.
|