Negative Exponents and Scientific Notation
- Having successfully defined 0 as an exponent, it seems
reasonable (to a mathematitian) to define negative
integers as exponents next.
As before, we look to the quotient rule as our guide. To
decide how to define a negative exponent, look at a quotient in
which the power on the bottom is bigger than the power on the
top.
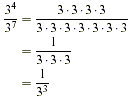
Now look at the same problem, but try applying the quotient
rule to it instead:
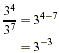
Thus, it makes sense to say that 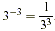
Definition (Negative Integers as Exponents)
For any real number a ( a 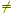 0) and any integer n, 0) and any integer n, 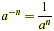
- Note that there is no negative sign on the right-hand
side of the equation in the definition above.
- This definition also tells us that
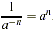 (Why?) (Why?)
- The usual rules for powers hold with this definition.
- Scientists often deal with very large (such as
93,000,000,000,000) and very small numbers (such as
0.00000000000113). To help deal with it, they have a
special notation, called scientific notation
which they use to write these numbers.
Definition (Scientific Notation)
Scientific notation for a number is an
expression which looks like N ×10 n, where 1 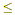 N <10 and n is any integer. N <10 and n is any integer.
This means that any number written properly in scientific
notation will have a single nonzero digit before the decimal
place.
|