Rules for Arithmetic With Approximate Numbers

The reason we have to be concerned with concepts such as exact and approximate numbers, and significant digits, precision and accuracy of approximate numbers, is to make sure that when we work with numbers representing actual measurements of physical quantities, we understand specifically what these numerical digits are telling us about the size of the physical quantity. In particular, it is important to avoid writing down digits in such a number which really convey no meaningful or justifiable information. This is really a topic that requires more detailed discussion than is possible in these notes. However, perhaps one hypothetical example will give you an insight into this issue.

Suppose the goal was to get an “accurate” measurement of the length of an object. Ten people are recruited, and each given an instrument to measure lengths. They report the following values:

963 mm 958 mm 961 mm 955 mm 959 mm

964 mm 962 mm 958 mm 960 mm 961 mm

Now, although a couple of pairs of these measurements are the same, there is also quite a variation in results, ranging from a low value of 955 mm to a high value of 964 mm. In this situation, we would have to conclude that we really don’t know the length of the object precise to 1 mm, since at that level of precision, there is no general agreement between the ten measurements. To be honest then, it appears we should state the result as 960 mm, meaning that the true length could be as much as 5 mm shorter or 5 mm longer than this value. So, to say that this object is 958 mm long might be misleading, since the data we have doesn’t narrow the length down more precisely than “some value between 955 mm and 965 mm”.

This example illustrates in a superficial way that it is important to be wary of stating results with an unwarranted number of significant digits when they are based on either measurements or calculations involving approximate numbers. What we will state below are the simplest of rules for deciding when digits in the result of a calculation are not really warranted and so should be discarded (through rounding-off).

For simple arithmetic calculations, there are two rules for rounding results obtained from approximate numbers:

Rule 1: When two or more approximate numbers are added and/or subtracted, the result is rounded to the precision of the least precise approximate number involved.

Rule 2: When two or more approximate numbers are multiplied and/or divided, the result is rounded off to the accuracy of the least accurate approximate number involved.

In practice, one does the entire calculation first, getting an overall result. Then the rules are applied as appropriate to round this final result. We do not do any rounding before the final result is obtained.

 

Example 1:

Compute the result of

528.63 + 816.4 – 921.072

Assume that each of these numbers are approximate numbers.

solution:

Just entering these numbers into a calculator gives the apparent result 423.958. Since this calculation involves only addition and subtraction, we need to use the precision of the three numbers involved to decide rounding for the final result (Rule 1). Now

528.63 has a precision of 2 decimal places

816.4 has a precision of 1 decimal place

921.072 has a precision of 3 decimal places.

The smallest precision here is one decimal place, for the second number, 816.4. Therefore the final result must be rounded to just one decimal place, giving 424.0.

 

Example 2:

Compute the result of

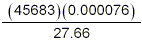
assuming each number is an approximate number.

solution:

When we enter these numbers into a calculator, the result is something like 0.125520896 (in this case, with a calculator having a 10-digit display – if we had a calculator with a 25-digit display, we’d get 0.1255208966015907447577730, so obviously there is no avoiding the question of having to round off the result of this calculation in some way!)

This calculation involves only multiplications and divisions, so it is the accuracy of the individual numbers which determines the accuracy of the result (Rule 2). Here

45683 has an accuracy of 5 significant digits

0.000076 has an accuracy of 2 significant digits

27.66 has an accuracy of 4 significant digits

We see that the least accurate number is the second one, 0.000076, with an accuracy of two significant digits. Therefore, by Rule 2, the final result should be rounded to two significant digits, giving 0.13.