Multiplication Property of Equality
When addition and multiplication are mixed in problems we will first apply the
Addition
Property vertically using a pattern (or balance beam ), where we work on each side of
the equation at the same time. When we get to the step where there is a constant on one
side and a variable multiplied by a coefficient not equal to one we will apply the
Multiplication Property.
2.3a.Constant multiplied on both sides:
A x = B or A = B x
(A, B are letters to represent integers.)
Recall that
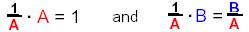
2.3b Find the variable x. To solve the equation we will keep the variable x on that side of
the equation and move the constant to the other side. To do this multiply reciprocals to
the entire equation or (both sides of the equation). First look at the pattern then follow
the same steps through the example below.
Solving Equations using the Multiplication Property of Equality
Pattern:
| Solve |
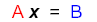 |
Multiply recip: |
| |
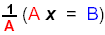 |
Distributive Property |
| |
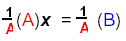 |
Associative Property |
| Then |
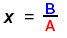 |
Since
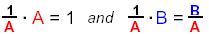 |
Example1
| Solve |
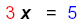 |
Multiply recip: |
| |
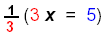 |
Distributive Property |
| |
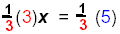 |
Associative Property |
| Then |
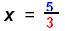 |
Recall
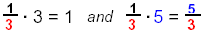 |
| Check: |
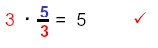 |
Replace x with
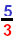 and simplify. and simplify. |
2.3c.Constant multiplied on both sides:
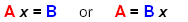
(A, B are letters to represent fractions.)
Recall that
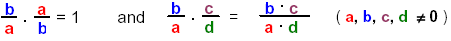
i) Simplify the equation so that there are only integers on both sides
2.3d. Find the variable x. To solve the equation we will keep the variable x on that side of
the equation and move the constant to the other side. To do this multiply reciprocal
fractions to the entire equation or (both sides of the equation). First look at the pattern
then follow the same steps through the example below.
|