Solving Inequalities
Solving Inequalities by Using Addition and Subtraction
| |
For all numbers a, b, and c, the
following are true. |
| Addition and Subtraction
Properties of Inequalities |
- If a > b, then a + c > b + c and a - c >
b - c. (Also true for
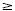 ) )
- If a < b, then a + c < b + c and a - c <
b - c. (Also true for
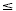 ) )
|
The solutions of an inequality can be graphed on a number line
or writtenusing set-builder notation
Example
Solve 3 m - 7 > 4 m + 1. Check your solution, and graph it
on a number line.
Solution
3m - 7 > 4m + 1
3m - 7 - 3m > 4m + 1 - 3m
- 7 > m + 1
- 7 - 1 > m + 1 - 1
- 8 > m or m < -8
In set builder notation, the solution set is {m | m < -8,
which is read "the set of all numbers m such that m is less
than -8". Only numbers less than - 8 substituted into the
original inequality should yield a true statement.
Since only the number less than - 8 yields a true statement,
the solution checks.Graph the point - 8 using an open circle,
since - 8 is not part of the solution.Then draw a heavy arrow to
the left to indicate numbers less than - 8.
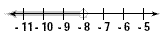
Solving Inequalities by Using Multiplication and Division
When you multiply or divide each side of an inequality by a
negative number, you must reverse the direction of the inequality
symbol.
| |
For all numbers a, b, and c, the
following are true. |
| Multiplication and Division
Properties for Inequalities |
- If c is positive and a < b, then ac < bc
and
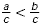 , and if c is positive
and a b, then ac > bc and , and if c is positive
and a b, then ac > bc and 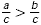 . .
- If c is negative and a < b, then ac > bc
and ,
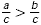 and if c is negative and
a > b, then ac < bc and and if c is negative and
a > b, then ac < bc and 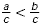 . .
|
These properties also hold true for inequalities involving 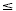 and and
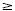 . .
Example
Solve -5 y 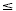 12 and check your solution. 12 and check your solution.
Solution
-5 y 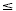 12 12
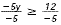 Divide each side by -5 and change the Divide each side by -5 and change the 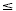 to
to 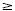 . .
Check: Let y be � 2.4 and any number
greater than -2.4, such as 0.
-5(-2.4) 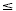 12 12 |
-5(0) 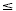 12 12 |
12 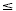 12 12 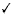 |
0 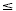 12 12 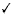 |
In set builder notation, the solution set is { y | y 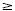 2.4} .
2.4} .
|