Solving Linear Systems of Equations by Substitution
Example
Use substitution to find the solution of this system.
|
-3x + 4y
x - 6y |
= 17 = -8 |
First equation
Second equation |
Solution
Step 1 Solve one equation for one of the variables in terms of the
other variable.
| Either equation may be solved for either variable.
For instance, let’s solve the second equation for x.
Add 6y to both sides. |
x - 6y
x |
= -8
= 6y - 8 |
Step 2 Substitute the expression found in Step 1 into
the other equation. Then, solve for the variable.
| Substitute 6y - 8 for x in the first equation.
Remove parentheses.
Combine like terms.
Subtract 24 from both sides.
Divide both sides by -14.
Now we know
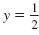 . .
Next, we will find x. |
-3x + 4y
-3(6y - 8) + 4y
-18y + 24 + 4y
-14y + 24
-14y
y |
= 17 = 17
= 17
= 17
= -7
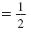 |
Step 3 Substitute the value obtained in Step 2 into one of the equations
containing both variables. Then, solve for the remaining
variable.
| We will use the equation from Step 1.
|
x |
= 6y - 8 |
Substitute
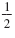 for y. for y.
|
x
|
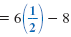 |
| Simplify.
The solution of the system is
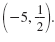 |
x |
= -5 |
Step 4 To check the solution, substitute it into each original equation.
Then simplify.
Substitute -5 for x and
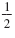 for y into each original equation. for y into each original equation.
Then simplify.
In each case, the result will be a true statement.
The details of the check are left to you.
Note:
If we graphed the system, the lines would
intersect at the point
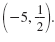
|