Powers

If a is any number and n any positive integer (whole number ) then the product of a with itself n times, 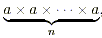, is called a raised to the power n, and written a ⁿ ; i.e.,

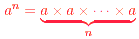
The following important rules apply to powers.

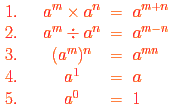
We want these rules to be true for all positive values of a and all values of m and n:

We shall first look at the simpler cases.

Examples

(a) 10 ² × 10 ³ = (10 × 10) × (10 × 10 × 10) = 10 ⁵ = 10 ²⁺³:

(b) 2 ⁵ ÷ 2 ³ = 32 ÷ 8 = 4 = 2 ² = 2 ^5-3

(c) ( 3 ² ) ³ = (3 × 3) ³ = (3 × 3) × (3 × 3) × (3 × 3) = 3 ⁶ = 3 ^{2 × 3}

(d) From rule 2, a ^{n + 1} ÷ a ⁿ = a ^{( n + 1) - n} = a ¹. Also,

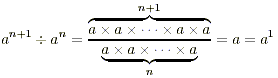
(e) We have a ⁿ × a ⁰ = a ^{n +0} = a n = a ⁿ × 1 : Thus a ⁰ = 1.