Positive and Negative Slopes
A line with a positive slope slants upward as we move from left to right on
the graph.
Each line shown has a positive slope.
To verify this, we can choose any two points on a line and find the slope.
For example, we will find the slope of line A.
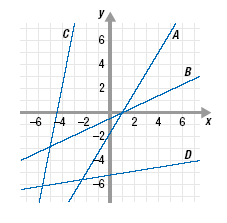
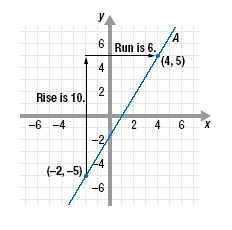
Example 1Find the slope of line A.
Solution
Choose any two points on line A.
For example, choose (-2, -5) and (4, 5).
| Let (x1, y1) = (-2, -5) and (x2, y2)
= (4, 5). |
m |
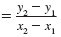 |
| Substitute the values in the slope formula. |
|
 |
| Simplify.
|
|
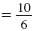 |
| Reduce. |
|
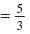 |
The slope of line A is a positive number,
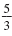 . . |
|
|
Line A slants upward as we move from left to right on the graph, so we
expected a positive slope.
A line with a negative slope slants downward as we move from left to right
on the graph.
Each line shown has a negative slope.
To verify this, we can choose any two points on a line and find the slope.
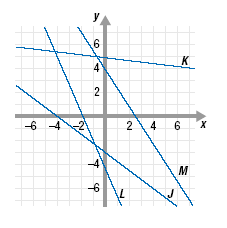
For example, we will find the slope of line J.
Example 2
Find the slope of line J.
Solution
Choose any two points on line J. For example, choose (-4, 0) and
(4, -6).
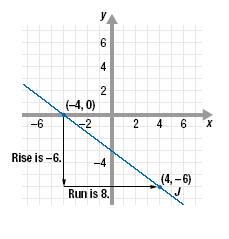 Line J slants downward as we move from left to right on the graph, so we
expected a negative slope.
|