Equations Quadratic in Form
In the next example we have a fourth-degree equation that is quadratic in form.
Note that the fourth-degree equation has four solutions.
Example 1
A fourth-degree equation
Solve x4 - 6x2 + 8 = 0.
Solution
Note that x4 is the square of x2. If we let w = x2, then w2
= x4. Substitute these expressions
into the original equation.
| x4 - 6x2 +
8 |
= 0 |
|
| w2 - 6w + 8 |
= 0 |
Replace x4 by w2 and x2
by w. |
| (w - 2)(w - 4) |
= 0 |
Factor. |
| w - 2 |
= 0 |
or |
w - 4 |
= 0 |
|
| w |
= 2 |
or |
w |
= 4 |
|
| x2 |
= 2 |
or |
x2 |
= 4 |
Substitute x2 for w. |
| x |
= ±
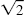 |
or |
x |
= 2 |
Even-root property |
Check. The solution set is {-2, -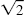 , ,
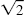 ,
2}. ,
2}.
Caution
If you replace x2 by w, do not quit when you find the values
of w. If the variable in the original equation is x, then you must solve for x.
Helpful hint
The fundamental theorem of
algebra says that the number
of solutions to a polynomial
equation is less than or equal
to the degree of the polynomial.
This famous theorem
was proved by Carl Friederich
Gauss when he was a young
man.
|