Zero Exponent
We have used positive and negative integral exponents, but we have not yet seen the
integer 0 used as an exponent. Note that the product rule was stated to hold for any
integers m and n. If we use the product rule on 23 · 2-3, we get
23 · 2-3 = 20.
Because 23 � 8 and
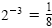 , we must have 23
· 2-3 = 1. So for consistency we
define 20 and the zero power of any nonzero number to be 1. , we must have 23
· 2-3 = 1. So for consistency we
define 20 and the zero power of any nonzero number to be 1.
Zero Exponent
If a is any nonzero real number, then a0 = 1.
Example
Using zero as an exponent
Simplify each expression. Write answers with positive exponents and assume all
variables represent nonzero real numbers.
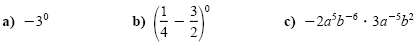
Solution
a) To evaluate -30, we find 30 and then take the opposite. So
-30 = -1.
b)
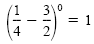 Definition of zero exponent Definition of zero exponent
| c) -2a5b-6 · 3a-5b2
|
= -6a5 · a-5 · b-6
· b2 = -6a0b-4
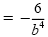 |
Product rule
Definitions of negative and zero exponent
|
Helpful Hint
Defining a0 to be 1 gives a consistent
pattern to exponents:
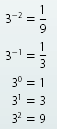
If the exponent is increased by
1 (with base 3) the value of the
expression is multiplied by 3.
|