Representing Simple Arithmetic Symbolically

The transition from mathematical expressions involving just numbers as in

5 + 3

to mathematical expressions involving symbols (which stand for unknown or unspecified numbers) such as

x + 3

is the most difficult step in mastering the methods of basic algebra. We can easily visualize what “5 + 3” means:

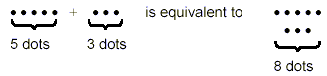
The group of 8 dots in the figure on the right clearly contains 3 more dots than the group of 5 dots on the left. It is obvious from these simple diagrams that when we compare

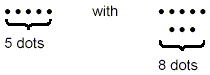
that the group of 8 dots can be described in relation to the group of 5 dots using any of the following phrases:

3 dots added to 5 dots
3 dots plus 5 dots
3 dots more than 5 dots
the sum of 3 dots and 5 dots
5 dots increased by 3 dots
a total of 5 dots and 3 dots
the 8 dots exceed the 5 dots by 3 dots

and so on. The clear point is: we started with a group of 5 dots and ended up with a group consisting of those original 5 dots plus another 3 dots (which we know from our knowledge of the meaning of words such as “one,” “two,” “three,” etc. – which are themselves just symbols – that the final group of dots happens to be what we call “eight” dots or 8 dots).

The expression

x + 3

has much the same interpretation:

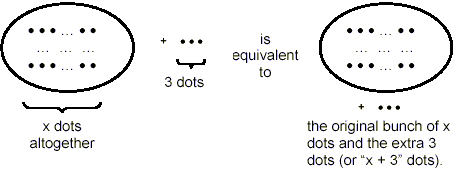
In this case, instead of starting out with a specific number of dots, such as the 5 dots in the earlier example, we’re just saying: “start with a certain number of dots,” and for convenience, we’ll represent the number of dots with which we actually start by the symbol x. Whatever the actual number of dots present in this group of x dots, the notion of adding another 3 dots to the pile of dots is easy to picture. We would have the original pile of x dots and now there would be 3 more dots in the pile of dots. This is all that is meant by

3 dots added to x dots
3 dots plus x dots
3 dots more than x dots
the sum of 3 dots and x dots
x dots increased by 3 dots
a total of x dots and 3 dots
the x + 3 dots exceed the x dots by 3 dots

In this way, the algebraic expression

x + 3

is a way of writing down the result of starting with a certain number, x, of things, and adding to that collection 3 more of the same things. It is very important to notice that the symbol x stands for the number of dots. x does not represent “a dot” or “the dots.” x represents the number of dots.

By now, you’re probably wondering what possible point there could be to using alphabetic symbols for numbers whose value we either don’t know at present, or for numbers we do not want to restrict to a specific actual value at present.

In many problems, we will be able to write down a very specific and concise representation of the answer despite not having enough information to reduce this final answer to a specific numerical value. Notice that

it doesn’t matter how many thing we start out with. That is, it doesn’t matter what value x actually may represent. If we include another three things, then the total number of things we end up with can be represented by the expression “x + 3” things.

it doesn’t matter what kind of “things” we are talking about as long as they are things we can count or measure numerically. In the four examples above, the “things” were numbers of dollars, numbers of kilometres, numbers of music CDs, and numbers of meters of rope. In each case, adding an additional three of these things to some original number of the same things can be represented by the same symbolic expression. This is because the symbol x represents a number of things rather than the things themselves.

These two observations give algebraic methods enormous usefulness in solving all sorts of problems involving numerical quantities. Not only do we have a way of representing unknown numerical values very clearly and concisely, but since these symbols represent actual numbers, we can to some extent use our knowledge of basic arithmetic with numbers to do arithmetic with these “unknowns.”

Of course, with numbers we can simplify expressions like “2 + 6” to 8 before multiplication by 4, so ultimately the use of brackets is avoided. However, with symbols, as in “x + 3”, it is not possible to do this – hence the requirement to use brackets is unavoidable.

Always, always, always, in algebra, the literal symbols represent numerical values. Often, being able to describe exactly what numerical value a symbol represents is the most important step in solving a problem.