Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

The Slope of a Line

Recall the RATIO of the y-difference (dy) to the x-difference (dx). Another name given to this RATIO is slope â€“designated m because the move is frequently on a slope up or down. We will examine its characteristics of this ratio and look at the equations for which we have built tables with the ratio of their differences.

When you draw a straight line, one of four things happen: [Read all graphs left to right.]

a)	b)	c)	d)
Goes up from left	Goes down from left	Is horizontal	Is vertical

By this time we have learned the relationship of the RATIO which determined the MOVE of our graph from one point to the next. We can determine the plot of the graph if we can find a starting place (point) and the ratio (move).

We have investigated the move up from a point dy (vertical difference between points) and over dx (horizontal difference between points) to the next point. The RATIO of the differences is called slope, always a "rational number" .

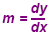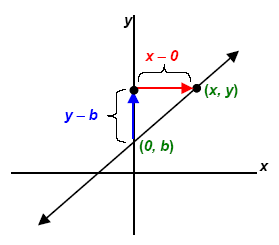
If we are given two points (0, b) and (x, y), we can FIND the slope m and we can WRITE the equation for the line in the slope-intercept form: y = mx + b



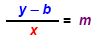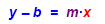	Multiply each side by x.
	Solve for y:

If we compare the values we have found in the these steps, we see that the value for m (move) and y-value ,b when x = 0 (y-intercept), appear in this new equation. In textbooks this is referred to as the slope-intercept form of a linear equation, which is the only FORMULA we really need.

y = m x + b