Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

The Product and Quotient Rules

The rules that we have already discussed are summarized below.

The following rules hold for nonnegative integers m and n and a ≠ 0.

a^m Â· aⁿ = a^{m + n}	Product rule
	Quotient rule
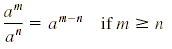	Quotient rule
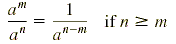a⁰ = 1	Zero exponent

Cuation

The product and quotient rules apply only if the bases of the expressions are identical. For example, 3² Â· 3⁴ = 3⁶, but the product rule cannot be applied to 5² Â· 3⁴. Note also that the bases are not multiplied: 3² Â· 3⁴ ≠ 9⁶.

Note that in the quotient rule the exponents are always subtracted, as in

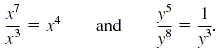
If the larger exponent is in the denominator, then the result is placed in the denominator.

Example 1

Using the product and quotient rules

Use the rules of exponents to simplify each expression. Assume that all variables represent nonzero real numbers.

Solution

a) Because the bases are both 2, we can use the product rule:

2³ Â· 2²	= 2⁵	Product rule
	= 32	Simplify

b) (3x)⁰(5x²)(4x)	= 1 Â· 5x² Â· 4x	Definition of zero exponent
	= 20x³	Product rule

c)	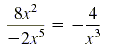Quotient rule

d) First use the product rule to simplify the numerator and denominator:

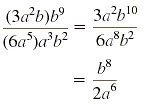	Product rule
	Quotient rule