Complex Numbers
In this section we define a set of numbers that has the real numbers as a subset.
Definition
The equation 2x = 1 has no solution in the set of integers, but in the set of rational
numbers, 2x = 1 has a solution. The situation is similar for the equation x2
= -4. It has no solution in the set of real numbers because the square of every real number
is nonnegative. However, in the set of complex numbers x2 = -4 has two solutions.
The complex numbers were developed so that equations such as x2 �4
would have solutions.
The complex numbers are based on the symbol
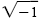 . In the real number system
this symbol has no meaning. In the set of complex numbers this symbol is given
meaning. We call it i. We make the definition that . In the real number system
this symbol has no meaning. In the set of complex numbers this symbol is given
meaning. We call it i. We make the definition that
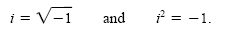
Complex Numbers
The set of complex numbers is the set of all numbers of the form a + bi,
where a and b are real numbers,
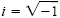 , and i2
= -1. , and i2
= -1.
In the complex number a + bi, a is called the real part and b is called the
imaginary part. If b � ≠ 0, the number a
+ bi is called an imaginary number.
In dealing with complex numbers, we treat a + bi as if it were a binomial, with
i being a variable. Thus we would write 2 + (-3)i as 2 - 3i. We agree that
2 + i3, 3i + 2, and i3 + 2 are just different ways of writing 2 + 3i (the standard
form). Some examples of complex numbers are
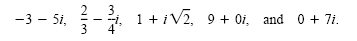
For simplicity we write only 7i for 0 + 7i. The complex number 9 + 0i is the real
number 9, and 0 + 0i is the real number 0. Any complex number with b = 0 is a
real number. For any real number a,
a + 0i a. The set of real numbers is a subset of the set of complex numbers.
Take a look at the figure below.
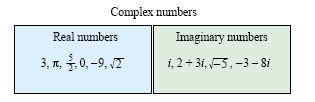
|