Free Algebra
Tutorials!

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

The Distance Formula

Consider the points (x₁, y₁) and (x₂, y₂) as shown in the figure below.

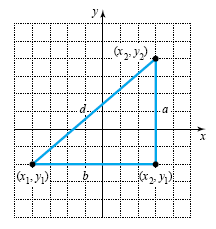
The distance between these points is the length of the hypotenuse of a right triangle as shown in the figure. The length of side a is y₂ - y₁ and the length of side b is x₂ - x₁. Using the Pythagorean theorem, we can write

d² = (x₂ - x₁)² + (y₂ - y₁)².

If we apply the even-root property and omit the negative square root (because the distance is positive), we can express this formula as follows.

Distance Formula

The distance d between (x₁, y₁) and (x₂, y₂) is given by the formula

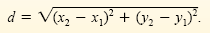
Example

Using the distance formula

Find the length of the line segment with endpoints (-8, -10) and (6, -4).

Solution

Let (x₁, y₁) = (-8, -10) and (x₂, y₂) = (6, -4). Now substitute the appropriate values into the distance formula:

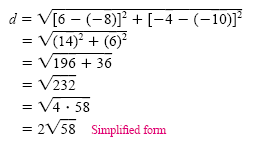
The exact length of the segment is .
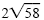