Powers of Complex Numbers

Positive Whole Number Powers

As an application of the rule for multiplying together complex numbers in polar form, it is a simple matter to multiply a complex number by itself any desired number of times.

Suppose that

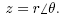
Then,

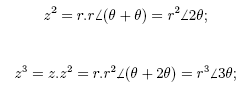
and, by continuing this process, 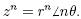This result is due to De Moivre, but other aspects of it will need to be discussed before we may formalise what is called “De Moivre’s Theorem”.

 

Example

 

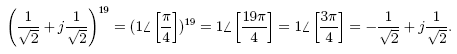
Negative Whole Number Powers

If n is a negative whole number, we shall suppose that n = −m, where m is a positive whole number.

Thus, if 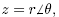then

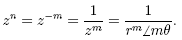
 In more detail,

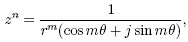
giving

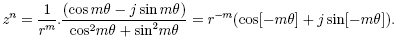
But −m = n, and so 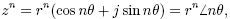showing that the result of the previous section remains true for negative whole number powers.

 

Example
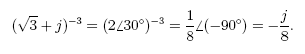