Negative Integral Exponents
If x is nonzero, the reciprocal of x is written as
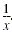For example, the reciprocal of 23 is written
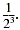To write the reciprocal of an exponential expression in a simpler way, we use a
negative exponent. So
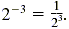In general we have the following definition.
Negative Integral Exponents
If a is a nonzero real number and n is a positive integer, then
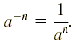(If n is positive, -n is negative.)
Example 1
Simplifying expressions with negative exponents
Simplify.
a) 2-5
b) (-2)-5
c)
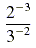
Solution
a)
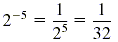
b)
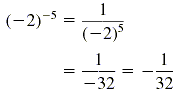Definition of negative exponent
c)
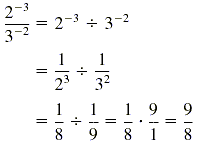
Caution
In simplifying -5-2, the negative sign preceding the 5 is used
after 5 is squared and the reciprocal is found. So
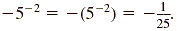
To evaluate a -n, you can first find the nth power of a and then
the reciprocal. However, the result is the same if you first find the reciprocal
of a and then find the nth power of the reciprocal. For example,
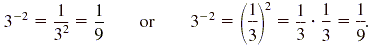
So the power and the reciprocal can be found in either order. If the exponent
is -1, we simply find the reciprocal. For example,
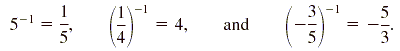
Because 3 -2 · 32 = 1, the reciprocal of 3 -2
is 32, and we have
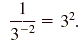
These expamples illustrate the following rules.
Rules for Negative Exponents
If a is a nonzero real number and n is a positive integer, then
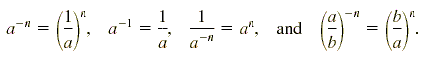
Example 2
Using the rules for negative exponents
Simplify
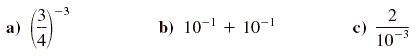
Solution
|
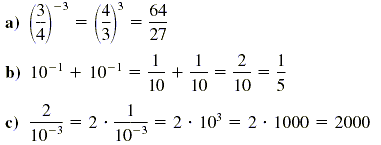
