Adding and Subtracting Polynomials
Like terms are terms that have the same variables raised to the same
power. Study the following examples.
| Like terms |
|
| 5x, -8x |
The variable part of each term is x.
|
| -9xy2, 3.7xy2 |
The variable part of each term is xy2
|
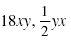 |
The variable parts, xy and yx, are equivalent.
|
| -1.5, 4 |
Constants are considered like terms. |
| Terms that are NOT like terms |
| 6x, -10xy |
The variables do not match.
|
| -7x3y3, 12x2y3 |
The powers of x do not match. |
To add polynomials, first remove any parentheses. Then combine like
terms.
Example 1
Find: (8x3 - 3x2 + 7x - 12) + (4x3 - 3x + 2)
| Solution |
(8x3 - 3x2 + 7x - 12) + (4x3 - 3x + 2) |
| Remove the parentheses. |
= 8x3 - 3x2 + 7x - 12 + 4x3
- 3x + 2 |
| Combine like terms.
|
= (8+4)x3 + (-3)x2 + (7-3)x + (-12 +
2) |
| Simplify. |
= 12x3 - 3x2 + 4x - 10 |
Then, the sum is 12x3 - 3x2 + 4x - 10.
Note:
We can also add polynomials in this way:
Line up like terms vertically.
Then add the coefficients.
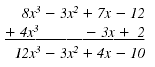
To subtract one polynomial from another, change the sign of each term in
the polynomial being subtracted. Then combine like terms.
For example:
8 - (2x - 3) becomes 8 - 2x + 3
(5x + 4) - (3x2 - x + 6) becomes 5x + 4 - 3x2 + x - 6
Note:
To subtract one polynomial from another,
add the first polynomial to the opposite of
the polynomial being subtracted.
Example 2
Find: (8x4 - 3x2y + 8x - 4) - (23x4 - 4x2y
+ 10)
| Solution |
(8x4 - 3x2y + 8x - 4) - (23x4 - 4x2y
+ 10) |
| Remove the parentheses. |
= 8x4 - 3x2y + 8x - 4 - 23x4
+ 4x2y - 10 |
| Combine like terms.
|
= (8 - 23)x4 + (-3 + 4)x2y + 8x +
(-4 - 10) |
| Simplify. |
= -15x4 + x2y + 8x - 14 |
So, the difference is -15x4 + x2y + 8x - 14.
Note:
We can also subtract polynomials
in this way:
Line up like terms vertically.
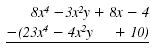
Then subtract the coefficients. To do this,
first change the sign of each term being
subtracted. Then add.
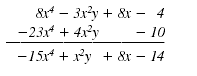
|