Negative Exponents
Objective Learn the notation of negative and
zero exponents.
The concept of exponentiation as repeated multiplication
cannot be extended to negative exponents. Therefore, this lesson
may be conceptually difficult.
Negative Numbers and Zero in the Exponent
First, let's review the rule for dividing powers that have the
same base.
Key Idea
When we divide a power of a by another smaller power of a, the
result is a power of a, where the exponent is the difference of
the exponents of the two dividends. In symbols,
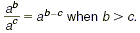
Only exponentiation with positive integers has been defined.
We have not discussed exponentiation with zero or with negative
numbers. In the formula
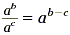
what happens if we no longer insist that b be greater than c?
What definition would this suggest to us for zero and negative
exponents?
If we applied the formula for b = c, we would get
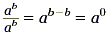
On the other hand,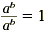 
. So, the formula suggests that a 0
= 1.
Key Idea
For any nonzero number a, a 0 = 1.
What does the equation shown above suggest about negative
numbers?
Let's consider a -1. According to the formula, we
have
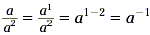
On the other hand,
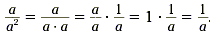
So the formula suggests that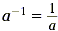 
. In general, we define a -n as
.
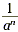Key Idea
For any nonzero number a and any integer n ,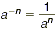 
.
You may be confused by the way the formula is used to generate
a definition for negative powers. It is used as a guide to
suggest what a definition should be, but that once we make the
definition, we can work with these exponents in exactly the same
way as we did with positive exponents. With this definition,
these exponents satisfy all the laws of exponents previously
studied.
The following formula shows what happens when b is less than
c.
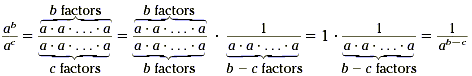
