Solving Nonlinear Equations by Substitution
An equation that can be solved using this approach is said to be
reducible to quadratic form.
Procedure —
To Solve an Equation Reducible to Quadratic Form
Step 1 Write the equation in quadratic form. Step 2 Use an appropriate “u†substitution.
Step 3 Solve the resulting equation.
Step 4 Substitute the original expression for u.
Step 5 Solve for the original variable. The letter u is traditionally used when
solving an equation by the substitution
method.
You may use a different letter if
you prefer.
Example
Solve for x: x4 - 21x2 - 35 = 65
| Solution
Step 1 Write the equation in quadratic form.
Subtract 65 from both sides.
Write x4 as (x2)2.
Step 2 Use an appropriate “u†substitution.
Substitute u for x2. |
x4 - 21x2 - 35
x4 - 21x2 - 100
(x2)2 - 21(x2)1 - 100
u2 - 21u - 100 |
= 65
= 0
= 0
= 0 |
| Use the Zero Product Property.
Solve each equation for u.
Step 4 Substitute the original
expression for u.
Step 5 Solve for the original variable. |
u + 4 = 0 or u - 25
u = -4 or u
x2 = -4 or x2 |
= 0 = 25 = 25 |
| Take the square root of both sides. |
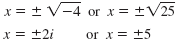 |
So, there are four solutions: -2i, +2i, -5, and +5. Needless to say, these
are the same solutions that we would obtain using factoring.
Note:
The exponent of x4 is twice
that of x2. So, we let u = x2.
Then, x4 = (x2)2 = u2.
|